Introduction
Neural networks are the foundation of deep learning, and mastering their basics is mandatory for every ML engineer in 2025. At CuriosityTech.in (Nagpur, Wardha Road, Gajanan Nagar), we emphasize not just theory, but stepwise understanding of how neurons compute, propagate, and learn.
Think of a neural network as a mathematical brain, where each neuron processes input, applies weights, activation functions, and passes results forward. Understanding this process deeply is essential before tackling advanced architectures like CNNs, RNNs, or Transformers.
1. Components of a Neural Network
| Component | Description | Analogy |
| Input Layer | Receives raw features | Senses (eyes, ears) |
| Hidden Layer(s) | Computes intermediate representations | Thinking process in the brain |
| Neuron (Node) | Computes weighted sum + bias | Brain neuron firing |
| Weights & Biases | Learnable parameters | Synaptic strengths |
| Activation Function | Adds non-linearity | Neuron firing threshold |
| Output Layer | Produces predictions | Decision/action |
2. Step-by-Step Computation in a Single Neuron
Forward Propagation:
For a single neuron with inputs x1,x2,x3x_1, x_2, x_3x1,x2,x3 and weights w1,w2,w3w_1, w_2, w_3w1,w2,w3, bias bbb:
- Compute weighted sum:
- z=w1x1+w2x2+w3x3+bz = w_1x_1 + w_2x_2 + w_3x_3 + bz=w1x1+w2x2+w3x3+b
- Apply activation function f(z)f(z)f(z) (e.g., ReLU, Sigmoid):
- a=f(z)a = f(z)a=f(z)
- Output aaa is sent to the next layer
Scenario Storytelling: Riya at CuriosityTech Park builds a simple network to predict whether a student passes based on study hours, sleep, and stress level. Each neuron computes weighted contributions and decides the next step.
3. Activation Functions Explained
| Function | Formula | Pros | Use Case |
| Sigmoid | σ(z)=11+e−z\sigma(z) = \frac{1}{1 + e^{-z}}σ(z)=1+e−z1 | Smooth gradient, outputs 0–1 | Binary classification |
| Tanh | tanh(z)=ez−e−zez+e−z\tanh(z) = \frac{e^z – e^{-z}}{e^z + e^{-z}}tanh(z)=ez+e−zez−e−z | Centered at 0, better for hidden layers | Regression and classification |
| ReLU | f(z)=max(0,z)f(z) = \max(0, z)f(z)=max(0,z) | Fast, avoids vanishing gradient | Hidden layers in deep networks |
| Leaky ReLU | f(z)=max(0.01z,z)f(z) = \max(0.01z, z)f(z)=max(0.01z,z) | Solves dead neuron problem | Deep architectures |
At CuriosityTech.in, students implement all activation functions and visualize outputs for sample inputs to understand behavior.
4. Architecture of a Neural Network
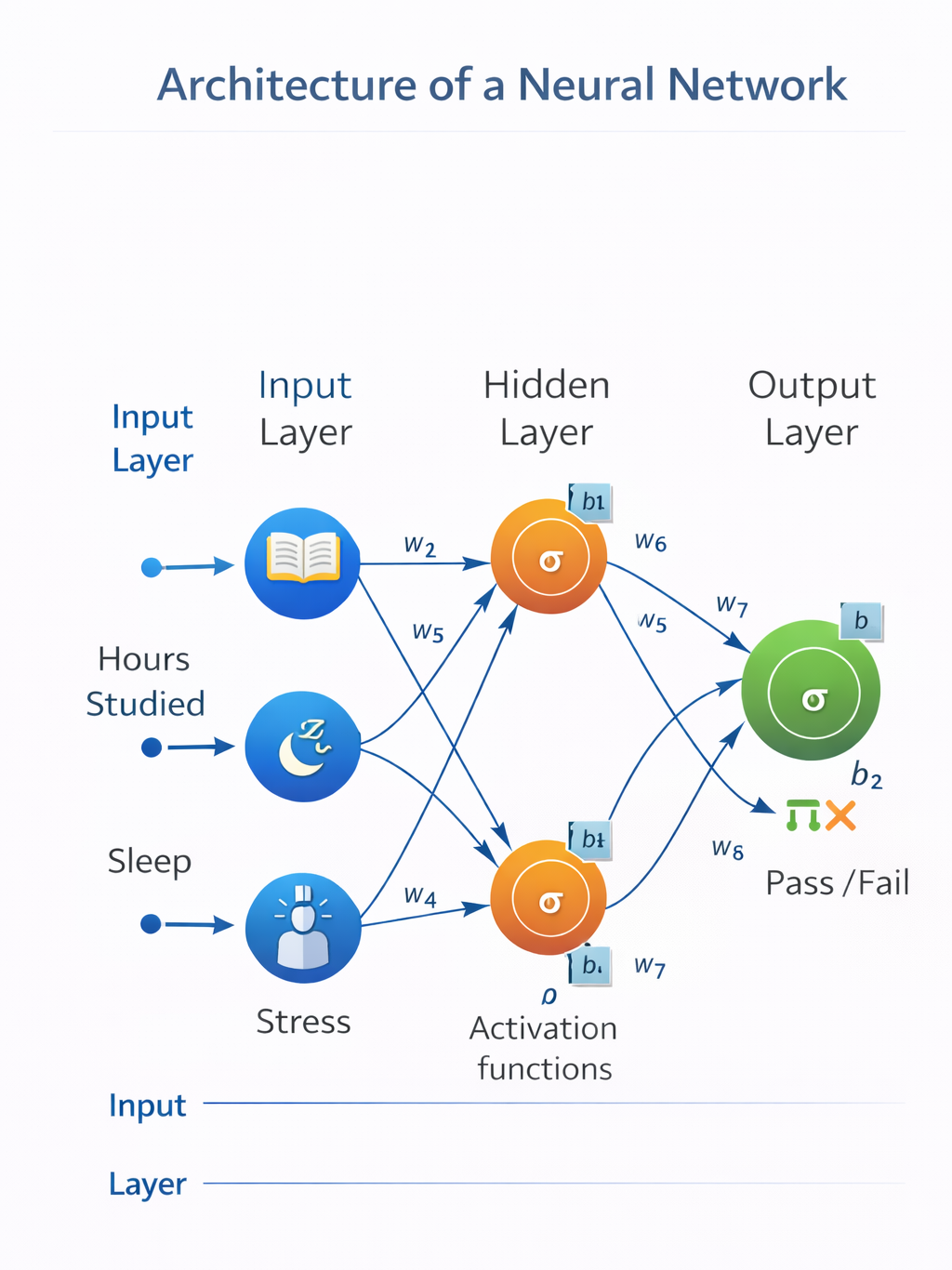
Description:
- Input layer: 3 nodes (features: hours studied, sleep, stress)
- Hidden layer: 2 neurons with weighted connections from inputs
- Output layer: 1 neuron (pass/fail)
- Arrows labeled with weights
- Biases added to each neuron
- Activation functions applied at hidden and output layers
Forward pass walkthrough:
- Compute weighted sums at hidden neurons
- Apply activation functions
- Pass outputs to final layer neuron
- Apply activation function to final output
5. Loss Functions
Loss functions measure prediction error and guide training.
| Task | Loss Function | Formula |
| Regression | Mean Squared Error (MSE) | 1n∑(yi−y^i)2\frac{1}{n} \sum (y_i – \hat{y}_i)^2n1∑(yi−y^i)2 |
| Binary Classification | Binary Cross-Entropy | −1n∑[yilogy^i+(1−yi)log(1−y^i)]-\frac{1}{n}\sum [y_i \log \hat{y}_i + (1-y_i)\log(1-\hat{y}_i)]−n1∑[yilogy^i+(1−yi)log(1−y^i)] |
| Multi-class Classification | Categorical Cross-Entropy | −∑yilog(y^i)-\sum y_i \log(\hat{y}_i)−∑yilog(y^i) |
CuriosityTech Insight: Students learn that choosing the correct loss function is crucial for convergence and accuracy.
6. Backpropagation (Weight Update)
Step-by-Step:
- Compute loss LLL using output and target
- Calculate gradients ∂L∂w\frac{\partial L}{\partial w}∂w∂L for each weight.
- Update weights using gradient descent:
- w=w−η⋅∂L∂ww = w – \eta \cdot \frac{\partial L}{\partial w}w=w−η⋅∂w∂L
- η\etaη = learning rate
Scenario: Arjun at CuriosityTech Nagpur trains a network on the MNIST dataset. He tracks weight changes across epochs, visualizing how the network learns digit patterns gradually.
7. Neural Network Training Pipeline
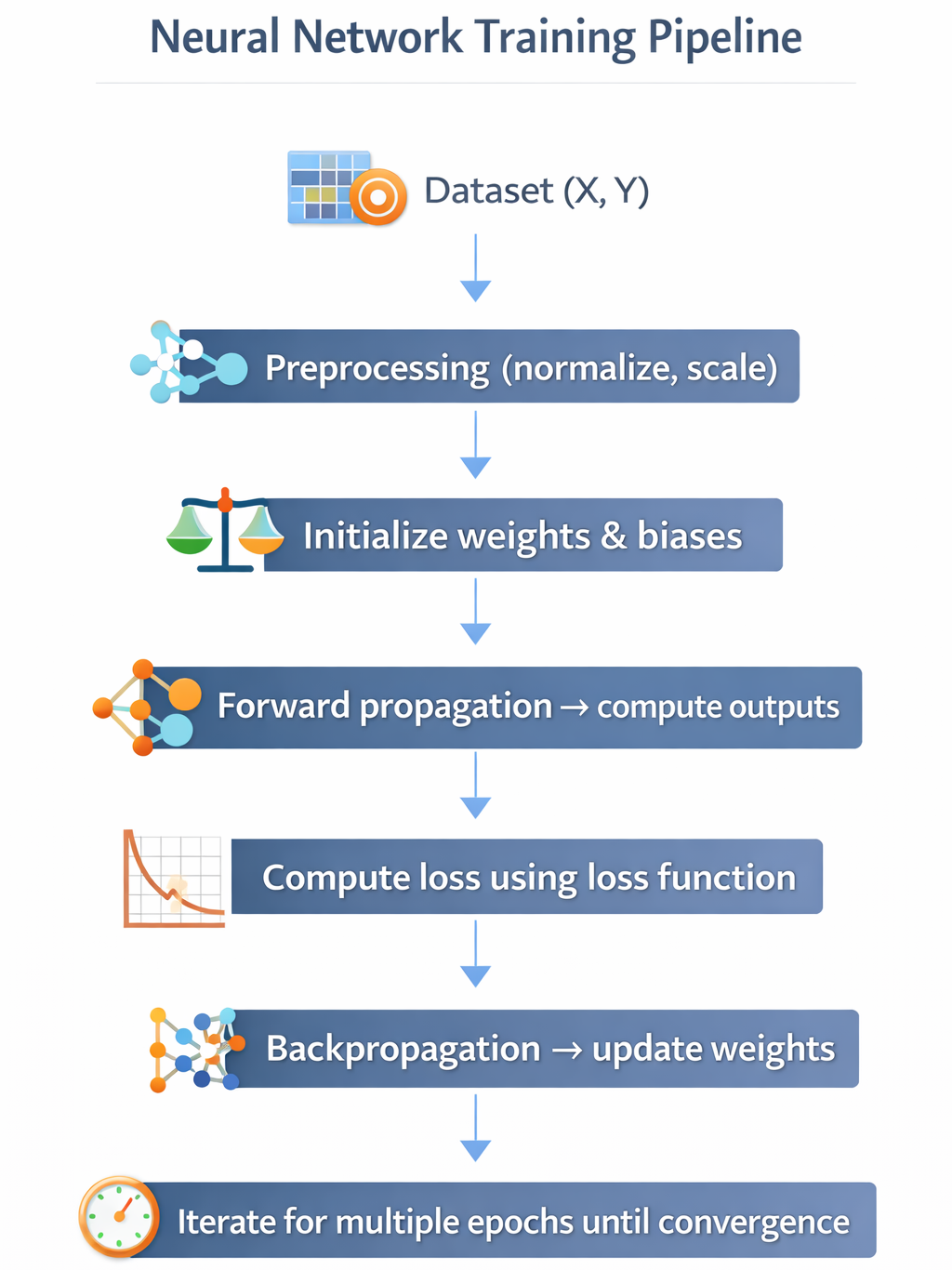
CuriosityTech Note: Students practice tracking accuracy and loss over epochs, which is critical to identify overfitting and underfitting.
8. Common Mistakes & Tips
| Mistake | Consequence | Correct Approach |
| Learning rate too high | Divergence, unstable training | Start small, use learning rate scheduler |
| Not normalizing inputs | Slower convergence, unstable | StandardScaler or MinMaxScaler |
| Too many/few neurons | Underfitting/overfitting | Experiment with layers and neurons |
| Ignoring overfitting | Poor generalization | Use dropout, regularization, early stopping |
9. Real-World Applications
| Application | Neural Network Type |
| Handwritten Digit Recognition | Feedforward NN |
| Sentiment Analysis | RNN, LSTM |
| Image Classification | CNN |
| Predicting Stock Prices | Feedforward + LSTM |
| Anomaly Detection | Autoencoder |
CuriosityTech.in students often implement step-by-step neural networks on these applications, gaining hands-on expertise.
10. Key Takeaways
- Neural networks are composed of layers, neurons, weights, and activations.
- Forward propagation and backpropagation are mandatory to understand for model training.
- Correct activation functions, loss functions, and learning rates significantly impact performance.
- Hands-on experimentation is the fastest way to mastery.
Conclusion
Neural networks form the core of modern AI and deep learning applications. By mastering the basics:
- You can design and train networks from scratch
- Understand how complex architectures like CNNs, RNNs, and Transformers work
- Transition confidently to real-world, production-ready ML projects
At CuriosityTech Nagpur, students gain layer-by-layer insights, visualizations, and practical training, ensuring readiness for industry challenges. Contact +91-9860555369 or contact@curiositytech.in to start hands-on neural network training.



